Los modelos de regresión logística aplicados a las ciencias de la salud nos permiten el análisis de los resultados en términos explicativos y predictivos, pudiendo conocer la fuerza de asociación mediante los OR de los factores de riesgo con el efecto estudiado de una manera independiente y conocer el valor predictivo de cada uno de ellos o bien del modelo en su conjunto. Pero hay que ser conscientes de que son una herramienta más en el método científico y que no subsanan problemas de diseño del estudio. Su uso, cada vez más frecuente debe ir precedido de una reflexión crítica tanto de la elección de las variables incluidas en el modelo como del análisis de sus resultados.
INTRODUCCIÓN
Con el nombre de modelos de regresión se incluyen un conjunto de técnicas estadísticas que tratan de explicar cómo se modifica la variable dependiente o resultado, cuando cambian otra u otras variables, denominadas independientes o predictoras. Lo que caracteriza en principio a las distintas clases de modelos de regresión es la naturaleza de la variable dependiente; así, con variables continuas la clase de modelos de regresión lineal es la más utilizada; con variables dicotómicas lo es el modelo de regresión logística.
La regresión logística (RL) es uno de los instrumentos estadísticos más expresivos y versátiles de que se dispone para el análisis de datos en clínica y epidemiología1. Su origen se remonta a la década de los sesenta (Confield, Gordon y Smith 1961); su uso se universaliza y expande desde principios de los ochenta debido, especialmente, a las facilidades informáticas con que se cuenta desde entonces. En los últimos años se ha verificado una presencia muy marcada de esta técnica, tanto en la literatura orientada a tratar temas metodológicos como en los artículos científicos biomédicos. Fiel reflejo de esta tendencia, es que el empleo de la RL suponía el 32% de los artículos publicados por American Journal of Epidemiology de 1986 a 1990 y el 68% de los que aparecieron en el mencionado quinquenio en New England Journal of Medicine, con lo cual quedó ubicada en el quinto puesto, solo superada por cuatro técnicas convencionales: t de Student, prueba Chi-cuadrado, análisis de la varianza y prueba de Fisher2.
En nuestro país, la evaluación de los artículos publicados en Medicina Clínica entre 1962 y 1992 refleja una escasa utilización de los análisis multivariantes3 aunque se aprecia una tendencia al alza4,5
Similar tendencia hemos observado al revisar los artículos originales de Nefrología de 1993 a 1999, apreciándose que los análisis de regresión logística sólo se emplearon en el año 99 (3 artículos), si bien analizando este mismo año (38 artículos) el 73,6% utilizan exclusivamente modelos estadísticos univariantes frente a un 26,3% que realizan análisis multivariante. De estos últimos, el 60% se centra en métodos de supervivencia. En general, parece observarse la popularización del uso de diversos análisis multivariantes, como la regresión logística, la regresión de Cox y otros análisis de supervivencia.
El conocimiento de estas técnicas permitiría al lector la compresión de los artículos publicados en revistas médicas, con el fin de obtener el máximo beneficio de la lectura y ser capaz de evaluar el mérito, validez y las conclusiones de la investigación publicada y posteriormente, decidir si las mismas son aplicables a su propia práctica y experiencia.
¿QUÉ ES LA REGRESIÓN LOGÍSTICA?
Los métodos de regresión de variable dependiente cualitativa abarcan diferentes modelos que tratan de explicar y predecir una característica cualitativa a partir de los datos de otras variables conocidas, bien cuantitativas o cualitativas que actúan como variables explicativas6.
La característica que se quiere explicar puede ser: a) una cualidad que puede únicamente tomar dos modalidades (modelos binomiales), son las más frecuentemente utilizadas, b) una cualidad que puede tomar más de dos modalidades diferentes, exhaustivas y mutuamente excluyentes (modelos multinomiales), c) una característica con varias modalidades que presentan entre ellas un orden natural (modelos ordenados) y d) la característica a explicar corresponde a una decisión que puede suponer decisiones encadenadas (modelos anidados).
Como es conocido, el concepto de regresión hace referencia a la ley experimental o fórmula matemática que traduce la relación entre variables correlacionadas. Generalmente cuando se quiere poner una variable en función de otra (o de otras), se acude al bien conocido recurso de la regresión lineal (simple o múltiple). Esta función utiliza normalmente el método de mínimos cuadrados y funciona fluidamente desde el punto de vista aritmético.
Pero cuando la variable a explicar sólo puede tomar dos valores, es decir, la ocurrencia o no de un cierto proceso, al evaluar la función para valores específicos de las variables independientes se obtendrá un número que será diferente de 1 y de O (los valores posibles de la variable dependiente), lo cual carece de todo sentido. En este caso, la regresión lineal debe ser descartada, en cambio la RL se ajusta adecuadamente a esta situación.
Mediante la RL se pretende es la probabilidad de que ocurra el hecho en cuestión como función de ciertas variables que se presumen relevantes o influyentes. Por lo tanto, la RL consiste en obtener una función logística de las variables independientes que permita clasificar a los individuos en una de las dos subpoblaciones o grupos establecidos por los dos valores de la variable dependiente.
La función logística es aquella que halla, para cada individuo según los valores de una serie de variables (Xi), la probabilidad (p) de que presente el efecto estudiado. Una transformación logarítmica de dicha ecuación, a la que se le llama logit, consiste en convertir la probabilidad (p) en odds. De aquí surge la ecuación de la regresión logística, que es parecida a la ecuación de la regresión lineal múltiple.
¿DÓNDE Y CUÁNDO APLICARLA?
La RL se utiliza cuando queremos investigar si una o varias variables explican una variable dependiente que toma un carácter cualitativo. Este hecho es muy frecuente en medicina ya que constantemente intentamos dar respuesta a preguntas formuladas en base a la presencia o ausencia de una determinada característica que no es cuantificable sino que representa la existencia o no de un efecto de interés, como por ejemplo el desarrollo de un «evento cardiovascular», «un paciente hospitalizado muere o no antes del alta», «se produce o no un reingreso», «un paciente desarrolla o no nefropatía diabética», etc. Una de las ventajas de la RL es que permite el manejo de múltiples variables independientes (también llamadas covariables) con un número reducido de casos1. Freeman (1987) ha sugerido que el número de sujetos debe ser superior a (10)(k+1), donde k es el número de covariables. Pero hay que tener en cuenta que el tamaño de la muestra necesaria es inherente al tipo de estudio que se realiza.
Como hemos mencionado anteriormente la RL tiene una doble función: explicativa y predictiva.
Podemos usarla con finalidad descriptiva siendo posible ofrecer una descripción elocuente y útil, basándonos en una información reducida; un ejemplo clásico es cuando la probabilidad que se estima puede interpretarse como una tasa de prevalencia o de incidencia que dependa de una variable continua. Aunque hay estudios que ejemplarizan este enfoque hay que reconocer que esta variante ha sido poco explotada1.
Su utilización en la predicción es el uso más frecuente y extendido, enmarcado en los diferentes tipos de estudios, ya sean típicamente prospectivos con finalidad pronóstica (epidemiología clínica), estudios prospectivos con finalidad analítica (cohortes), estudios caso-control (riesgo atribuible) y en los ensayos clínicos. Quisiéramos en este punto resaltar que la RL es un instrumento muy útil para facilitar el tratamiento cuantitativo de los datos pero no podemos aislarlo del diseño del estudio, so pena de cometer errores que nos conducirían a conclusiones erróneas.
Hay que destacar que además de predecir riesgos, la RL puede servir para estimar la fuerza de la asociación de cada factor de riesgo de una manera independiente, es decir, eliminando la posibilidad de que un factor confunda el efecto de otro7.
¿CÓMO INTERPRETARLA?
No es pretensión de este artículo desarrollar en profundidad todas las posibilidades de interpretación de los resultados ya que existen numerosos manuales publicados al efecto8,9. Pero sí acercarnos a los parámetros que contengan una mayor utilidad clínica.
Cuando realizamos una RL lo que pretendemos es estimar los parámetros de la ecuación (β0, β1, β2,...βk) de la función que pretendemos evaluar:
Z =β0 + β1X1 + β2X2 +... +βkXk
Donde Z es el logaritmo neperiano (Ln) de la odds de padecer la enfermedad, el desenlace o el resultado que se está estudiando; β0 es la ordenada en el origen de la función de regresión, β1, β2,...βk representan los coeficientes de la pendiente de la recta y X1,X2,...Xk son las variables independientes o factores de riesgo. Si nuestros datos se ajustan de manera satisfactoria a este modelo, tendremos la suerte de poder explicar la relación entre las variables independientes y la respuesta de una manera muy sencilla. Los coeficientes βi expresan el logaritmo neperiano del odds ratio (OR) para cada factor de riesgo Xi. Por tanto el OR se estima a partir de la fórmula:
OR = antilog (βi) = eβi
Una vez que hemos construido nuestro modelo de RL, debemos primero analizar los coeficientes de regresión (βi) de cada variable independiente para obtener sus OR y luego confeccionar el valor predictivo de cada variable independiente o bien del modelo en su conjunto.
Con el siguiente ejemplo práctico, intentaremos aproximarnos a estos conceptos. Consideremos un modelo de regresión logística para analizar la probabilidad de desarrollar enfermedad coronaria o no, en base a la contribución de los siguientes factores de riesgo: fumador, diabético, hipertenso, razón colesterol/hdl colesterol > 5 y presentar insuficiencia renal, medida por el aclaramiento de creatinina (FG).
Ahora nos plantearemos dos objetivos:
1º. Conocer la fuerza de asociación, a través de los OR, de cada uno de los factores de riesgo con el efecto estudiado de una manera independiente, es decir, eliminando la posibilidad de que un factor confunda el efecto de otro.
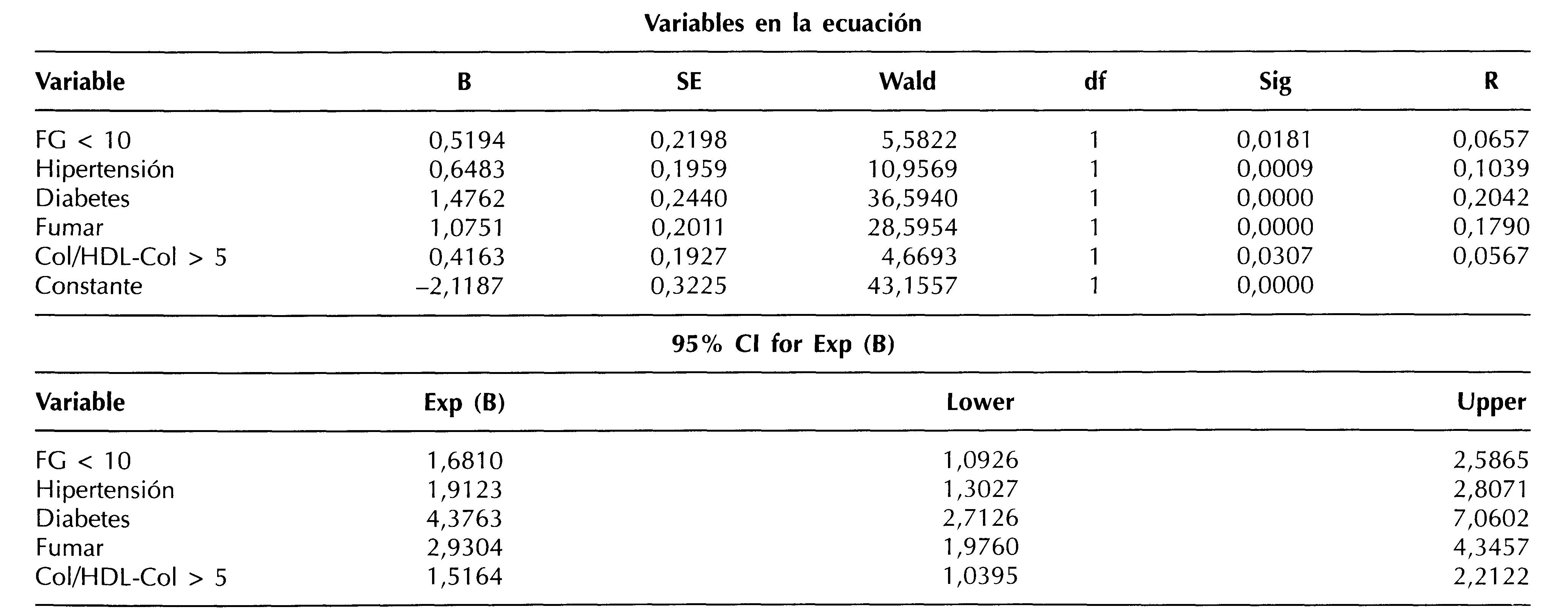
Una vez obtenidos los coeficientes de regresión logística (βi = β) de cada una de las variables del modelo (tabla I), lo que tenemos es Ln (OR) del ser fumador (1,075), diabético (1,4762), etc., ya que como sabemos Bi = Ln (OR).
Para saber la fuerza de asociación (medida en OR) de la enfermedad coronaria con las variables incluidas en el modelo de RL, sólo necesitamos calcular su antilogaritmo, o lo que es lo mismo hallar su exponencial, ya que
OR = antilog (βi) = eβi
Hoy en día están disponibles diversos paquetes estadísticos (SAS, LIMDEP, SPSS) que facilitan estos cálculos. Uno de los más utilizados es el SPSS al que haremos referencia en cuanto a sus salidas en este artículo. Este programa nos permite obtener los coeficientes de regresión βi (B), los errores estándar de los coeficientes (SE), el nivel de significación (Sig) de cada coeficiente a través del estadístico de Wald [testa la hipótesis de si los coeficientes son iguales a O, si sigue una distribución Χ2 con sus grados de libertad (df)], el coeficiente de correlación parcial (R) que es una forma de ver la influencia de cada una de las variables independientes por separado con la variable dependiente, y los exponenciales de los coeficientes [Exp (B)] que como sabemos son los OR de cada variable independiente con sus intervalos de confianza al 95% o al nivel que nosotros previamente hallamos estipulado (tabla I).
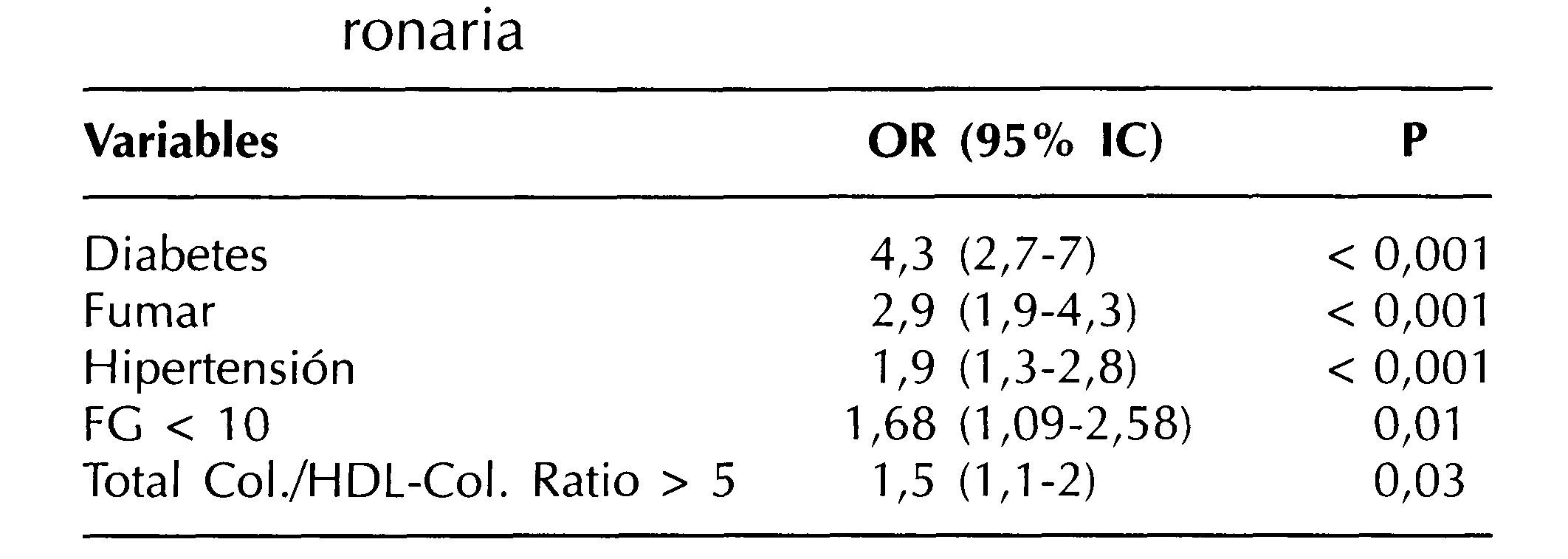
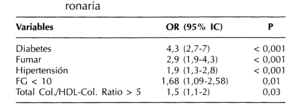
De esta manera sabremos que el riesgo de padecer una enfermedad coronaria es 4,3 veces mayor si se es diabético que si no se es, 2,9 por ser fumador o 1,9 por ser hipertenso. Hay que recalcar que los valores de los OR están ajustados, es decir, se elimina la posibilidad de que un factor confunda el efecto de otro (tabla II).
2º. Confeccionar el valor predictivo de cada variable independiente o bien del modelo en su conjunto.
Siguiendo el ejemplo anterior, abordaremos ahora como obtener el valor predictivo del riesgo asociado a padecer una enfermedad coronaria, para ello partiremos de la ecuación siguiente:
Z = β0 + βiXi + β2X2... + βkXk
Z = Ln (odds)
Ln (odds) = -2,1187 + (0,6483 X hipertensión) + (1,4762 X diabetes) + (1,0751 X tabaco) + (0,4163 X Col/HDL-col > 5) + (0,5794 X FG < 10)
La primera cifra corresponde a la constante del modelo (β0) y las variables independientes (Xi) ser hipertenso (Sí=1, No=0), ser diabético (Sí=1, No=0), ser fumador (Sí=1, No=0), tener una razón colesterol total / HDL colesterol mayor de 5 (Sí=1, No=0) y un aclaramiento de creatinina menor de 10 ml/min (Sí=1, No=0) para un indivisuo que reúna todas estas condiciones tendremos:
Ln (odds) = -2,1187 + (0,6483 x 1) + (1,4762 x 1) + (1,0751 x 1) + (0,4163 x 1) + (0,5194 x 1)
Ln (odds) = 2,0166
Odds = antilog (2,0166) = e2,0166 = 7,5127
p = odds / 1 + odds
p = 7,5127 / 8,5127 = 0,8825
La ecuación predice un riesgo del 88,2% de padecer una enfermedad coronaria en aquellos pacientes que presenten hipertensión, diabetes, fumen, tengan una razón colesterol total/HDL-colesterol mayor de 5 y un aclaramiento de creatinina menor de 10 ml/min.
Pero si solo presenta el riesgo de tener un aclaramiento de creatinina menor de 10 ml/min sería de 16,8% y si sólo fuera diabético la probabilidad de padecer una enfermedad coronaria ascendería al 34,4%.
Ln (odds)GFR < 10 = -2,1187 + (0,6483 x 0) + (1,4762 x 0) + (1,075 x 0) +( 0,4163 x 0) + (0,5194 x 1)
Ln (odds) = -2,1187 + 0,5194 = -1,5993
Odds = antilog (-1,5993) = e-1,5993 = 0,2020
p = odds / 1 + odds
p = 0,2020 / 1,2020 = 0,1680
Ln (Odds)Diabetes -2,1187 + (0,6483 x 0) + (1,4762 x 1) + (1,0751 x 0) + (0,4163 x 0) + (0,51940)
Ln (odds) = -2,1187 + 1,4762 = -0,6425
Odds = antilog (-0,6425) = e-0,6425 = 0,5259
p = odds / 1 + odds
p = 0,5259/1,5259 = 0,3446
En el ejemplo propuesto todas las variables independientes son categóricas, pero es frecuente su combinación con variables continuas, siendo su cálculo el mismo, salvo que multiplicaríamos por el valor del factor de riesgo considerado (colesterol mg/dl, edad en años, peso en kg, etc.).
Hemos analizado dentro de la RL como interpretar los coeficientes de regresión desde la perspectiva anglosajona, a través de los odds asociados a cierto suceso (el riesgo de padecer una enfermedad coronaria siendo diabético es de 4,3) y desde la perspectiva del mundo latino, calculando la probabilidad de ocurrencia de un suceso (la probabilidad de sufrir una enfermedad coronaria siendo diabético es del 34,4%). De modo que ambas informaciones son equivalentes y expresan la misma noción: cuantifican cuán probable es que algo ocurra.
PRECAUCIONES
La RL como otras técnicas cuantitativas, y más desde la generalización del uso de potentes paquetes estadísticos, presentan el riesgo de que sean utilizadas de manera acrítica y muchas veces sin que el usuario comprenda totalmente lo que hace1. Por ello resaltaremos la importancia de la selección del modelo de RL, la necesidad de evaluar el modelo viendo los criterios de ajuste del mismo, el manejo de variables dummy y los problemas relativos a la colinearidad de las variables estudiadas.
Selección del modelo. Existen varios procedimientos de selección de variables en la RL (similares en cualquier tipo de regresión multivariada). El más usado es el de la regresión paso a paso (Stepwise Regression) que consiste en construir modelos sucesivos que difieren del precedente en una sola variable e ir comparándolos. El criterio de entrada o salida en el modelo es la significación estadística del coeficiente de regresión. Las dos variantes fundamentales del procedimiento son ir añadiendo variables (Forward Stepwise) o ir eliminando variables (Backward Stepwise), las variables van saliendo del modelo también una a una, pero a partir del modelo inicial en el que todas ellas están incluidas.
La elección del modelo va a depender del tipo de estudio, pero es preciso recordar el concepto de «variables relevantes». El modelo de RL que nos planteamos al realizar un estudio de investigación analítico debe pasar necesariamente por una reflexión de que variables incluidas en nuestro trabajo explican la variable dependiente objeto de nuestro interés. Y esto no pasa exclusivamente por un proceso de elección estadística, ya que esta técnica no distingue entre asociaciones de índole causal y las debidas a otros factores, incluso a las debidas a sesgos en el estudio10-12
Criterios de ajuste. Al realizar cualquier modelo de regresión, es preciso antes de sacar conclusiones corroborar que este modelo se ajusta efectivamente a los datos. Existen varios métodos: la tabla de clasificación, la verosimilitud (-2 Log Likelihood), o el estadístico de Goodness of Fit.
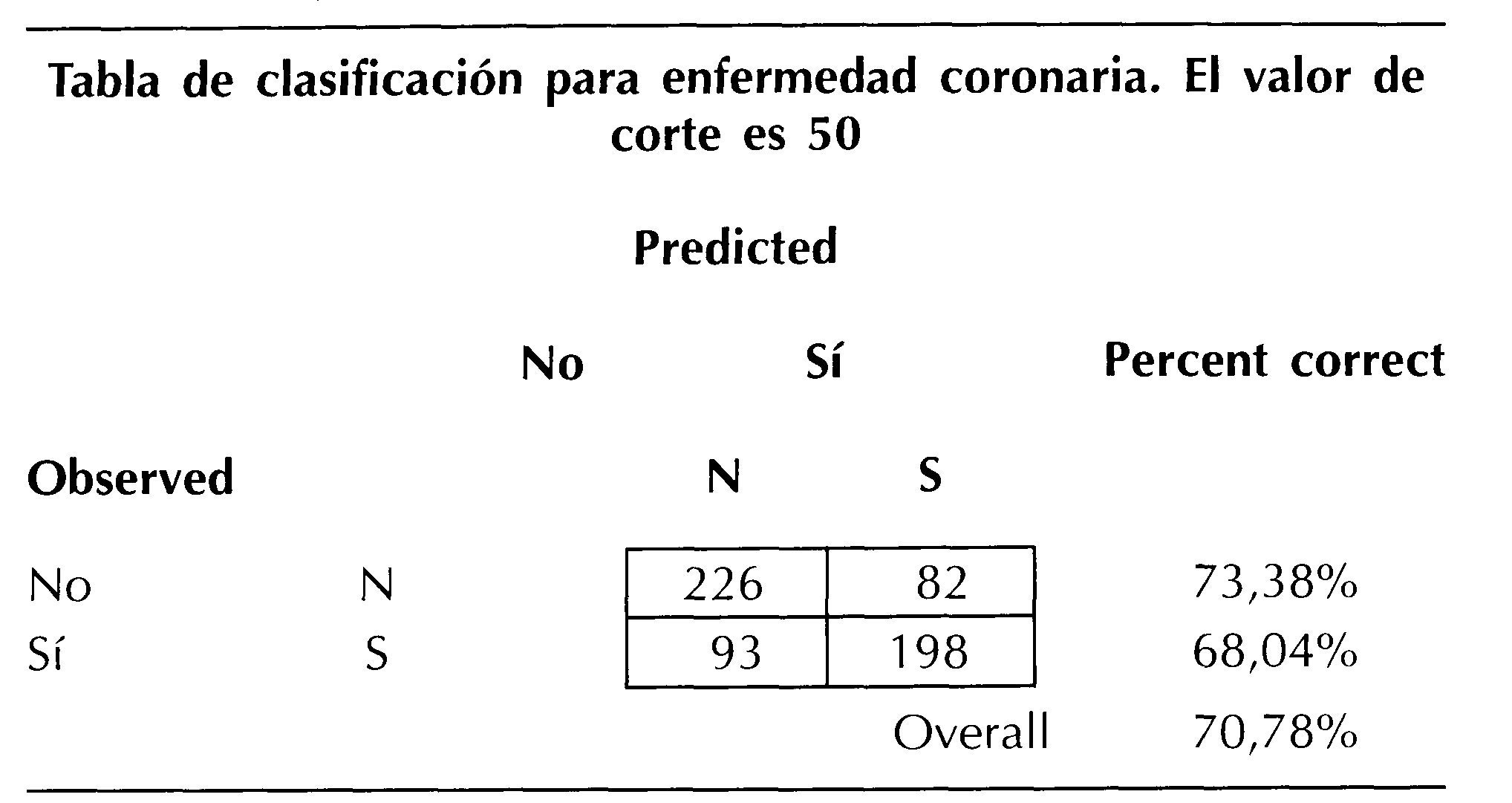
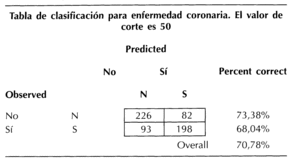
Quizá el más intuitivo es la tabla de clasificación que consiste en verificar qué porcentaje de individuos clasifica correctamente el modelo. Veamos un ejemplo (tabla III): tenemos un total de 599 individuos; de los 291 que sufren una enfermedad coronaria el sistema clasifica correctamente a 198 (verdaderos positivos) que suponen un porcentaje de clasificación correcta del 68,04% (sensibilidad del modelo); de los 308 que no padecen una enfermedad coronaria clasifica correctamente a 226 (verdaderos negativos) lo que supone un 73,38% (especificidad del modelo). En total 424 (verdaderos positivos más verdaderos negativos) son clasificados correctamente por el modelo, lo que supone un 70,78% de ajuste global. Ahora le corresponde al investigador decidir si el porcentaje de los clasificados correctamente le parece adecuado o no, aunque parece razonable aceptar modelos que clasifiquen correctamente alrededor del 70%.
Variables dummy. Son una serie de variables artificiales, también conocidas como variables de paja o variables ficticias, cuya finalidad es introducir como variables independientes a variables cualitativas con varias categorías, como por ejemplo la insuficiencia renal medida por el aclaramiento de creatinina (FG < 10, FG: 10-40 y FG: 41-100 ml/min). Para ello se crearán tres variables dummy (FG <10, FG: 10-40 y FG: 41-100) que nos darán información de presentar una determinada función de filtrado glomerular dentro del intervalo considerado o estar fuera de dicho intervalo (tener FG < 10 = 1, frente a no tenerla = 0). Cuando utilizamos estas variables ficticias debemos recordar que el conjunto de variables dummy son un todo indisoluble con el cual se suple una variable nominal y cualquier decisión que se adopte o valoración que se haga concierne al conjunto íntegro.
Colinearidad. Es un problema originado cuando las variables independientes del modelo están muy altamente correlacionadas, es decir, comparten entre sí la misma información.
Una solución natural es la de evitar la inclusión en el modelo de una variable cuando este ya contiene otras que aportan de hecho la información de aquella variable. Por ejemplo, incluir el peso y la talla de los individuos cuando incluimos el índice de masa corporal. El introducir todas estas variables juntas en el modelo, puede arrojar resultados poco fiables.
GLOSARIO
Variable dependiente: es la variable que refleja la ocurrencia o no del suceso. Es decir aquella característica que pretendemos explicar en función de otras variables, las llamadas variables explicativas. Las variables dependientes pueden ser cuantitativas o cualitativas. También reciben el nombre de «variables de resultado».
Variable independiente: es la variable que pretende explicar la variable dependiente. También reciben el nombre de «variables predictoras», «variables explicativas» o «covariables». Al igual que las variables dependientes pueden ser cuantitativas o cuantitativas.
Variable durnmy: son variables artificiales o ficticias, creadas a partir de la información de una variable independiente, para poder realizar operaciones matemáticas con ellas. De la variable original se pueden crear múltiples variables dummy, pero no debemos olvidar que son un todo indisoluble.
Proporción: es un cociente cuyo numerador está incluido en el denominador. Carece de unidades y sus valores oscilan entre O y 1. Pueden expresarse en tantos por uno, porcentajes, tantos por mil, etc.
Razón, Ratio: es un cociente cuyo numerador no está incluido en el denominador. Tengamos en cuenta que no existen restricciones en el rango de sus valores.
Odds: se trata de una razón en la que el numerador es la probabilidad (p) de que ocurra un suceso y en el denominador es la probabilidad de que tal suceso no ocurra (1-p). Es un caso particular de una razón. También recibe el nombre de «ventaja» o «razón de complementos».
Odds Ratio (OR): es el cociente o razón entre dos odds y carece de unidades de medida. El OR no tiene interpretación absoluta, siempre es relativa. Para poder interpretar una OR, es necesario siempre tener en cuenta cuál es el factor o variable predictora que se estudia y cuál es el resultado o desenlace. El valor nulo para la OR es el 1, esto implica que las dos categorías comparadas son iguales. También recibe el nombre de «razón de odds» o «razón de ventajas».
Riesgo relativo (RR): es la relación entre la incidencia dentro del grupo expuesto y la incidencia dentro del grupo no expuesto. El riesgo relativo es pues la medida del papel etiológico del factor de riesgo. La denominación riesgo relativo se debe a que es la relación entre dos riesgos (expuestos y no expuestos). Si el RR es 1, el factor estudiado no tiene papel causal. Para su cálculo es preciso conocer la incidencia, ya que ésta mide los casos nuevos en una población durante cierto período.
Intervalo de Confianza (IC) Confidence Interval (CI): es el intervalo dentro del que se encuentra la verdadera magnitud del efecto, nunca conocida exactamente, con un grado prefijado de seguridad. A menudo se habla de «intervalo de confianza al 95%» o «límites de confianza al 95%». Quiere decir que dentro de ese intervalo se encontraría el verdadero valor en el 95% de los casos.
Tabla 1. Resultados del modelo de regresión logística
Tabla 2. Estimación del riesgo para enfermedad coronaria
Tabla 3. Tabla de clasificación del modelo de regresión logística*