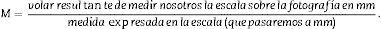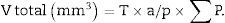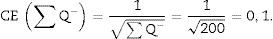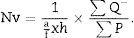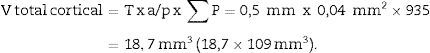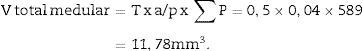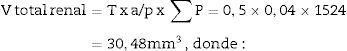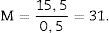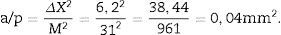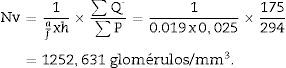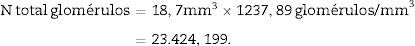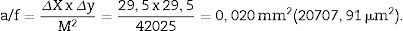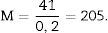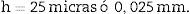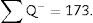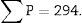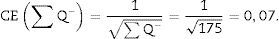Los riñones son órganos vitales que realizan funciones de excreción, equilibrio hidroelectrolítico y producción de hormonas. La nefrona es su unidad estructural y funcional. El número, tamaño y distribución de los componentes de la nefrona contienen información relevante sobre la función renal. La estereología es una rama de la morfometría que permite, aplicando reglas matemáticas, obtener información tridimensional de estructuras biológicas a partir de cortes microscópicos bidimensionales, seriados, paralelos y equidistantes. Ante la complejidad de los estudios estereológicos y la carencia de una bibliografía clara sobre el desarrollo de los mismos, el objetivo de este trabajo es explicar de forma sencilla y con ejemplos, utilizando un modelo animal, los conceptos básicos de estereología, así como el cálculo de los principales parámetros estereológicos renales y que estos puedan ser aplicados en futuros estudios experimentales.
The kidneys are vital organs responsible for excretion, fluid and electrolyte balance and hormone production. The nephrons are the kidney's functional and structural units. The number, size and distribution of the nephron components contain relevant information on renal function. Stereology is a branch of morphometry that applies mathematical principles to obtain three-dimensional information from serial, parallel and equidistant two-dimensional microscopic sections. Because of the complexity of stereological studies and the lack of scientific literature on the subject, the aim of this paper is to clearly explain, through animal models, the basic concepts of stereology and how to calculate the main kidney stereological parameters that can be applied in future experimental studies.
El riñón es un órgano esencial en el mantenimiento de la homeostasis, siendo la nefrona su unidad estructural y funcional. El número, tamaño y distribución de los componentes de la nefrona (glomérulos, túbulos…) aportan información importante acerca de la función renal, haciendo su cuantificación relevante en estudios frente a traumas, químicos y/o enfermedades. En estos casos, así como en situaciones de normalidad, los estudios estereológicos nos permiten detectar y cuantificar modificaciones macro o microscópicas1.
La estereología es una rama de la morfometría que permite, aplicando fórmulas matemáticas basadas en la probabilidad geométrica estadísticamente significativa, obtener información tridimensional de células o estructuras biológicas a partir de cortes microscópicos bidimensionales, seriados, paralelos y equidistantes2.
Dada la dificultad de los estudios estereológicos y la carencia de una bibliografía clara sobre el desarrollo de los mismos, el objetivo de este trabajo es explicar paso a paso, de forma sencilla y con ejemplos, utilizando un modelo animal, cómo calcular los principales parámetros estereológicos del riñón, y de esa forma sentar unas bases de fácil comprensión que puedan ser aplicadas en futuros estudios experimentales, contribuyendo así a la resolución de muchos problemas de patología, fisiología y bioquímica2,3.
Material y métodosPreparación de la muestraLos riñones de ratón son extraídos y fijados durante 24h en paraformaldehído al 4% a temperatura ambiente. Posteriormente se lavan con agua, se someten a sucesivos baños de alcohol etílico de concentraciones crecientes, se aclaran con xilol y se incluyen totalmente en parafina (cada riñón en un molde independiente). Una vez hechos los bloques, se conservan en archivadores a temperatura ambiente.
Elaboración de los cortes histológicosConviene empezar con un estudio piloto que incluya uno o 2 animales, para ir corrigiendo errores y ajustando los pasos (por ejemplo, cuántos campos utilizamos para medir glomérulos, cuántos disectores por campo histológico, etc.)4.
Colocamos un bloque con un riñón en el microtomo y lo seccionamos en su totalidad en secciones de 5 micras de espesor. Para el cálculo del volumen y la densidad numérica no influye la orientación1 (en nuestro laboratorio realizamos cortes transversales). Otro de los problemas que se puede plantear al abordar este objetivo es si es necesario, o no, que la corteza renal sea isótropa para aplicar el método, y si el tamaño de las partículas puede inducir a error.
Como se ha explicado previamente en artículos clásicos5, ese problema puede ser resuelto con el adecuado muestreo, que dé a cada partícula, en este caso glomérulos, la misma probabilidad de ser contada.
Seleccionaremos para el estudio estereológico las secciones o cortes n.o 100 y 106, 200 y 206,… y así sucesivamente hasta el final.
Solo escogeremos aquellos cortes que al extenderlos sobre el porta no estén rotos ni plegados. Si esto sucede en el corte que nos corresponda seleccionar, avanzaremos 5 micras o lo necesario hasta obtener un corte óptimo, siempre que luego se mantenga la distancia de 25 micras con su correspondiente sección pareada, y continuemos con el sistema establecido inicialmente.
Las secciones 100, 200… sirven para calcular el volumen total del riñón o volumen de referencia según Cavalieri, y las llamaremos «secciones volumen». Se obtienen de una forma sistemática (los cortes tienen siempre la misma distancia entre ellos o T), uniforme (son cortes paralelos entre sí) y al azar (el primer corte se escoge de forma arbitraria entre los cortes 0 y T, siendo T igual a 100 cortes en este caso). Es importante obtener un número mínimo de cortes (mayor o igual a 6) para poder obtener dicho volumen con un coeficiente de error aceptable1,3,4.
Las secciones 106, 206,… son secciones pareadas que utilizaremos para estimar la densidad numérica (n.o de glomérulos/mm3) según el método del disector físico. El motivo por el que estén separadas 6 cortes de su sección par («sección volumen») se debe a que la distancia óptima entre dichas secciones debe ser aproximadamente 1/3 del diámetro medio de la estructura a medir (en este caso, el glomérulo)6. En el caso de los glomérulos de riñón del ratón adulto correspondería a unas 25 micras aproximadamente7,8 (a 5 cortes de 5 micras de espesor). Las 2 secciones pareadas se colocan en el mismo porta.
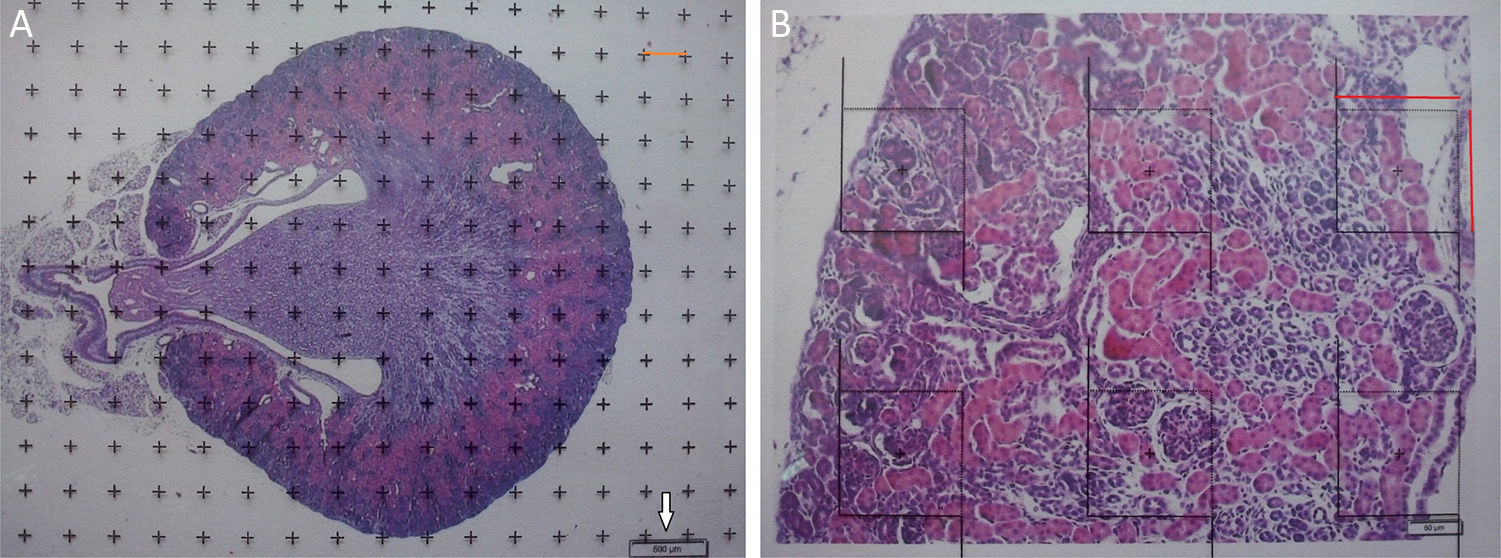
Análisis estereológicoPara calcular el volumen total realizaremos microfotografías de las «secciones volumen» donde pueda verse la totalidad del riñón (objetivos 1× y 1,25×). Cada fotografía debe incorporar su escala correspondiente. Sobre ellas superpondremos una malla de puntos de la que calcularemos la distancia entre cada punto o marca y lo llamaremos Δx, midiendo con un calibre su distancia en mm (fig. 1A). Una vez tenemos la malla sobre el riñón, contamos el n.o de puntos o marcas que «caen» encima de la imagen renal (lo llamaremos ∑P).
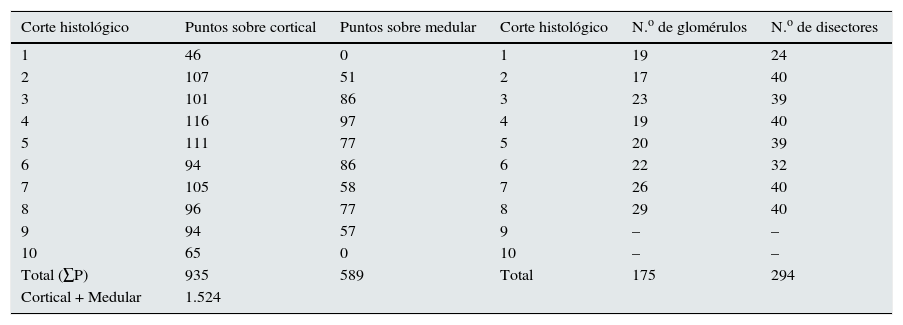
A) Microfotografía con objetivo 1,25× de corte transversal de riñón de ratón (hematoxilina-eosina), con malla de puntos superpuesta para recuento de puntos y cálculo del volumen según Cavalieri. Flecha blanca: escala presente para cálculo de la magnificación. Línea roja: Δx o distancia entre puntos. B) Microfotografía de un campo histológico con objetivo 10× de la corteza renal según corte transversal, con malla superpuesta con 6 disectores. Línea roja: Δx y Δy (iguales por ser un disector cuadrado).
Como la microfotografía puede ser mayor o menor según el tamaño del monitor donde se proyecte, utilizamos la escala de la fotografía para evitar que ello afecte al estudio, y la medimos sobre el monitor con un calibre. Con este valor podemos calcular la magnificación o M:
Ahora, ya podemos aplicar la siguiente fórmula:
T=distancia entre «secciones volumen».
a/p (área asociada a cada punto) =, Δx2 es la distancia entre dos puntos de la malla y M es la magnificación.
∑P=sumatorio de puntos que caen dentro de la estructura a medir (riñón), superponiendo una malla de puntos sobre la misma, en cada una de las fotografías resultantes (por ejemplo, si tenemos 6 «secciones volumen», entonces ∑P=∑P1 +…+∑P6).
Para el cálculo de la densidad numérica según el método del disector físico1,6,7 aplicamos una malla con los disectores sobre las microfotografías de los cortes 100, 200 … («secciones de referencia») y luego las comparamos con sus pareadas 106, 206…. (secciones «look up»). Para ello, hacemos 2 microfotografías (objetivo 10×) de cada sección pareada (siempre con la escala) que nos permitirán ver simultáneamente las 2 secciones. Una vez hemos localizado la misma zona histológica en ambos cortes pareados, superponemos la plantilla con los 6 disectores (podrían ser más o menos) en la imagen de referencia (100, 200…) y contamos cuántos glomérulos (∑Q¿) de la imagen de referencia (fig. 1A) caen dentro del marco de recuento (counting frame) sin tocar las líneas prohibidas (líneas rectas) y no aparecen en la imagen «look up» (fig. 1B).
Esto se debe realizar sobre 10 campos corticales aleatorios de cada «sección volumen» obtenida (buscando referencias histológicas para asegurar la misma localización en las 2 secciones pareadas).
Para que el estudio esté bien hecho, tenemos que contar entre 100-200 glomérulos o ∑Q¿, ya que así, al aplicar la fórmula para el cálculo del coeficiente de error o estimación en el error de la varianza, este tendría un valor aproximado de 0,1.
Por último, contamos el número de disectores (∑P) utilizados en el recuento de glomérulos para calcular sobre qué volumen de riñón se están contando los glomérulos. En el caso ejemplo serían: 60 disectores por cada «sección volumen» (6 disectores superpuestos sobre 10 campos histológicos) × n.o total de «secciones volumen» que hayamos obtenido.
Finalmente aplicamos la siguiente fórmula para obtener la densidad numérica:
a/f (área del marco de recuento o disector) = ΔX x ΔyM2.
h: distancia entre secciones pareadas del disector (en este caso, 25 micras).
∑Q¿: sumatorio de partículas o glomérulos contados según el disector, en todas las «secciones volumen».
∑P: sumatorio de disectores utilizados para medir los glomérulos, en todas las «secciones volumen».
Una vez tenemos la densidad numérica (Nv), podemos realizar una estimación del n.o total de glomérulos3,4:
N.o total de partículas=volumen total×densidad numérica (Nv).
ResultadosComenzamos seccionando el riñón de un ratón 0F1 adulto (Charles River, Barcelona, España) en secciones de 5 micras de espesor, con una T de 500 micras (lo que equivale a 100 cortes de separación entre «secciones volumen»).
Cálculo del volumen total según CavalieriDebido al tamaño del riñón, obtenemos 10 «secciones volumen» y las fotografiamos con un objetivo 1,25× en el microscopio, incorporando la escala (que para este objetivo corresponde a una escala de 500μm, y medida sobre la foto son 15,5mm).
Aplicamos la malla de puntos y hacemos el siguiente recuento (tabla 1).
Valores de los puntos sobre la corteza y la médula renal para el cálculo del volumen total del ejemplo. Y número de glomérulos y de disectores utilizados para el cálculo de la densidad numérica del ejemplo
| Corte histológico | Puntos sobre cortical | Puntos sobre medular | Corte histológico | N.o de glomérulos | N.o de disectores |
|---|---|---|---|---|---|
| 1 | 46 | 0 | 1 | 19 | 24 |
| 2 | 107 | 51 | 2 | 17 | 40 |
| 3 | 101 | 86 | 3 | 23 | 39 |
| 4 | 116 | 97 | 4 | 19 | 40 |
| 5 | 111 | 77 | 5 | 20 | 39 |
| 6 | 94 | 86 | 6 | 22 | 32 |
| 7 | 105 | 58 | 7 | 26 | 40 |
| 8 | 96 | 77 | 8 | 29 | 40 |
| 9 | 94 | 57 | 9 | – | – |
| 10 | 65 | 0 | 10 | – | – |
| Total (∑P) | 935 | 589 | Total | 175 | 294 |
| Cortical + Medular | 1.524 | ||||
Con esos datos podemos calcular:
T=500 micras o 0,5mm.
Cálculo de la densidad numérica con el disector físicoHacemos 2 microfotografías (objetivo 10×) de cada sección pareada (escala de 200 micras que mide 41mm). Localizamos la misma zona histológica en ambos cortes pareados, superponemos la plantilla con los 6 disectores en la «imagen o sección de referencia» (100, 200…) y contamos cuántos glomérulos (∑Q¿) caen dentro del marco de recuento (counting frame) sin tocar las líneas prohibidas (líneas rectas) y no aparecen en la imagen «look up» (sección pareada). Repetimos esta acción sobre 10 campos de cada «sección volumen o de referencia».
Contamos el n.o de disectores empleados y aplicamos la fórmula:
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Los autores agradecen su colaboración a los Dres. Jorge Arias y Marta Méndez, del departamento de Psicología de la Universidad de Oviedo, y en especial al profesor Dr. Luis M. Cruz-Orive, de la Universidad de Santander.