Introducción: La ecuación clásica Modification of Diet in Renal Disease (MDRD) subestima el filtrado glomerular en los valores más altos. Para aumentar su concordancia en los estadios 1 y 2 de la enfermedad renal crónica se ha establecido una nueva fórmula: la ecuación Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI). Objetivo: El objetivo del presente estudio es comprobar si la nueva ecuación es mejor que la MDRD en la estimación del filtrado glomerular en la insuficiencia renal crónica avanzada, en una población como la nuestra que tiene unas características antropométricas distintas de las de la población norteamericana. Material y métodos: En 89 pacientes con enfermedad renal crónica en estadios 4 y 5, hemos estudiado el grado de concordancia entre el filtrado glomerular medido como la media de los aclaramientos de urea y creatinina (AclUrCr) y el estimado por las ecuaciones MDRD, CKD-EPI y Cockcroft-Gault (CG). La concentración de creatinina corresponde a creatinina estandarizada. La variabilidad de cada una de las ecuaciones fue estudiada mediante la diferencia relativa (diferencia absoluta con el AclUrCr expresada como porcentaje de la media entre el AclUrCr y la ecuación analizada). Resultados: El filtrado glomerular medido por el AclUrCr y el estimado por las ecuaciones MDRD, CKD-EPI y CG fue respectivamente de 14,5 ± 5,5, 14,3 ± 5,5, 13,6 ± 5,4 y 16,8 ± 6,5 ml/min/1,73 m². No hay diferencia estadísticamente significativa del AclUrCr con la ecuación MDRD, pero sí con la ecuación CPK-EPI (p <0,01) y con la ecuación CG (p <0,001). La variabilidad de las diferentes ecuaciones con respecto al AclUrCr fue de 16 ± 12,2%, 16,7 ± 12,1% y 22 ± 15,6%, para las ecuaciones MDRD, CKD-EPI y CG, respectivamente (p <0,01 entre la ecuación CG y las dos ecuaciones previas). El porcentaje de mediciones que se encontraban dentro del 30% por encima o por debajo del valor conseguido con el método de referencia fue del 85% de las realizadas con la ecuación MDRD, del 88% con la ecuación CKD-EPI y del 70% de las realizadas con la ecuación CG. La variabilidad de las ecuaciones MDRD y CKD-EPI no se ve influida por el sexo, ni se correlacionó con la edad, el índice de masa corporal ni con el filtrado glomerular medido como AclUrCr. Por el contrario, la variabilidad de la ecuación CG era menor en hombres (19,3 ± 15,1 frente a 27,3 ± 15,5%; p <0,05) y tenía una correlación negativa con la edad (r = —0,24; p <0,05) y con el filtrado glomerular (r = —0,23; p <0,05), y positiva con el índice de masa corporal (r = 0,37; p <0,001). Conclusiones: Podemos concluir que en nuestra población con insuficiencia renal crónica avanzada, la ecuación CKD-EPI tiene una equivalencia con el filtrado glomerular medido como la media de los aclaramientos de urea y creatinina, similar al de la ecuación MDRD. Con la creatinina estandarizada, la ecuación CG pierde concordancia y su utilización debe ser reconsiderada.
Introduction: The aim of this work was to study the accuracy of the CKD-EPI equation to estimate the glomerular filtrate in patients with advanced chronic renal failure. Objective: We compared the estimations of Modification of Diet in Renal Disease (MDRD), Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) and Cockcroft-Gault (CG) equations to a glomerular filtration rate measured as the arithmetic mean of the urea and creatinine clearances (ClUrCr). Material and methods: The study was made in 89 nondialyzed patients with chronic renal disease in stage 4 or 5. Serum creatinine values were recalibrated to standardized creatinine measurements. In each patient, the difference between each estimating equation and the measured glomerular filtration rate was calculated. The absolute difference expressed as a percentage of the measured glomerular filtration rate indicates the intermethod variability. Results: Overall, the glomerular filtration rate measured as the ClUrCr was 14.5 ± 5.5 ml/min/1.73 m²; and the results of the estimating equations were: MDRD 14.3 ± 5.5 (p = NS); CKD-EPI 13.6 ± 5.4 (p <0.01) and CG 16.8 ± 6.5 ml/min/1.73 m² (p <0.001). The variability of the estimating equations was 16 ± 12.2%, 16.7 ± 12,1% and 22 ± 15.6% (p <0.05), for MDRD, CKD-EPI and CG. The percentage of estimates within 30% above or below the measured glomerular filtration rate was 85% for MDRD, 88% for CKD-EPI and 70% for CG. The CG variability, but not MDRD variability or CKD-EPI variability, was influenced by gender (19.3 ± 15.1% in males vs 27.3 ± 15.5% in females, p <0.05) and showed a negative correlation with the glomerular filtration rate (r = —0.23, p <0.05) and the age (r = —0.24, p <0.05) and positive correlation with the body mass index (r = 0.37, p <0.001). In patients with chronic renal disease in stage 5, the variability of the different estimating equations was similar. Conclusions: We conclude that in our population with advanced chronic renal failure, the CKD-EPI equation is as accuracy as the MDRD equation. With standardized creatinine the CG equation has a lower accuracy and its utilization may be reconsiderated.
INTRODUCTION
Glomerular filtration rate is estimated in clinical practice using equations obtained from serum concentrations of creatinine and other laboratory, demographic, and anthropometric values. The most commonly used formulas are the Cockcroft-Gault equation normalised for 1.73m2 (CG)1 and the abbreviated equation derived from the MDRD study (Modification of Diet in Renal Disease).2 Comparisons made between these two equations are highly debated, and depend on the population under study. In a previous study, we concluded that in the Spanish population with advanced chronic renal failure (stages 4 and 5), the CG equation has a better correlation with true glomerular filtration rate, as measured using urea and creatinine clearance rates, than the MDRD equation.3
One cause of error in the estimation of glomerular filtration rate was the variability in serum creatinine values produced by the different laboratory methods employed. In order to reduce this bias, the National Kidney Disease Education Program Laboratory Working Group proposed that laboratories use creatinine-based methods traceable to the isotope dilution mass spectrometry (IDMS) reference method.4 In general, a standardised serum creatinine concentration tends to be lower than the value obtained with previous methodologies. CG and MDRD equations were calculated using non-standardised creatinine measurements; as using standardised creatinine values, these equations yield higher glomerular filtration rates. Therefore, the MDRD formula was modified and adapted to a standardised creatinine value.5 The CG formula has not been re-evaluated for a standardised creatinine measurement.
The primary limitation to the MDRD equation is the tendency to underestimate glomerular filtration rate at higher values.6 In order to increase concordance in stage 1 and 2 chronic kidney disease, a new formula was established: the equation developed by the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI), using standardised creatinine measurement techniques, which, according to the authors, could replace the MDRD equation in clinical practice.7
The aim of this study was to test whether the new CKD-EPI equation is better than the MDRD in estimating glomerular filtration rate in advanced chronic renal failure patients, in a population such as ours that has different anthropometric characteristics to the North American population. We used the arithmetic mean of urea and creatinine clearance as our measure of glomerular filtration rate, which is the procedure recommended by clinical guidelines in this type of patient8-11 because of the good correlation with measurement methods based on exogenous substance clearance.12-15
MATERIAL AND METHOD
In May 2009, our laboratory in the nephrology department adopted a new standardised method for measuring creatinine levels. Since then, glomerular filtration rate has been estimated simultaneously using CG, MDRD, and CKD-EPI equations, all taken from blood samples.
Ours was a retrospective study performed using patients with chronic kidney disease in stages 4 and 5, attended to in the pre-dialysis unit between June 2009 and March 2011. Here, urea and creatinine clearance levels are systematically measured in urine samples 24 hours prior to extracting blood samples. Patients first receive oral and written instructions as to the correct urine sample taking. At the moment of performing the analysis, the patients are systematically questioned regarding the proper taking of the urine sample. When an error is suspected, clearance levels are not calculated and the sample is discarded. The formula for CG includes weight; as such, we also excluded patients with volume overload (presence of oedema or ascites). In all cases, we measured patient height and weight and calculated body surface area according to the Dubois and Dubois equation.16
We calculated glomerular filtration rate as the arithmetic mean of urea and creatinine clearance levels, and adjusted the value for a body surface area of 1.73m2 (ClUrCr). We also measured glomerular filtration rate using CG,1 abbreviated MDRD for standardised creatinine (MDRD-4 IDMS),5 and CKD-EPI.7 The CG equation was normalised for a body surface area of 1.73m2. We used only one single measurement for each patient (the first valid sample in the time period analysed).
Creatinine concentrations were measured in both serum and urine samples using an IDMS-traceable kinetic Jaffé method, and together with urea, they were analysed automatically using a Unicel DxC 800 machine by Beckman Coulter Inc. (Fullerton, California). The internal variation coefficients were the following: serum creatinine: 1.5% (for a mean concentration of 5.7mg/dl); urine creatinine: 2.2% (for a mean concentration of 143mg/dl); serum urea: 1.8% (for a mean concentration of 103mg/dl); urine urea: 2.6% (for a mean concentration of 1.617mg/dl).
Statistical analysis
We have expressed all results as a mean ± standard deviation (SD). The data analysed had a normal distribution (Kolmogorov-Smirnov test), and so we used parametric tests for the statistical analyses. The calculation of the difference, for each patient, between the glomerular filtration rate measured using each of the different formulas (CG, MDRD, and CKD-EPI), and ClUrCr in each patient allowed us to evaluate whether the equations under or overestimate the value of ClUrCr (bias). The difference, expressed as an absolute value, was used to evaluate the variation in the values. The value of absolute difference expressed as the percentage of the arithmetic mean between the ClUrCr value and that of each formula (relative difference) allowed us to evaluate the variability of each different equation (accuracy). We also measured the percentage of measurements for each equation that resulted in a value within 30% above or below the value obtained using the reference method (P30%). This parameter combines bias and accuracy, and was established by the Kidney Disease Outcomes Quality Initiative (KDOQI) as the best criteria for comparing the accuracy of the different equations in estimating glomerular filtration rate.17 The correlation between the different methods was tested using Pearson’s coefficient. We also used the intraclass correlation coefficient to evaluate concordance/equivalence, which is another test used to analyse the level of equivalence between the different methods of measurement.18
We compared means using Student’s t-tests and percentages using chi-square tests. Values of P<.05 were considered to be statistically significant.
RESULTS
Our study included a total of 89 patients (59 men and 30 women). Four patients were from South America (Colombia, Ecuador, and Peru), two from Romania, one from Morocco, and the other were born in Spain. None of the patients were of African descent, nor were any amputees. The aetiology of the renal failure was vascular in 26% of cases, diabetes in 21%, polycystosis in 8%, glomerulonephritis in 7%, interstitial in 5%, unknown in 15%, and other aetiologies in 18%. According to the ClUrCr values, 39 patients had stage 4 chronic renal failure (ClUrCr: 15-29ml/min/1.73m2) and 50 had stage 5 chronic renal failure (ClUrCr<15ml/min/1.73m2).
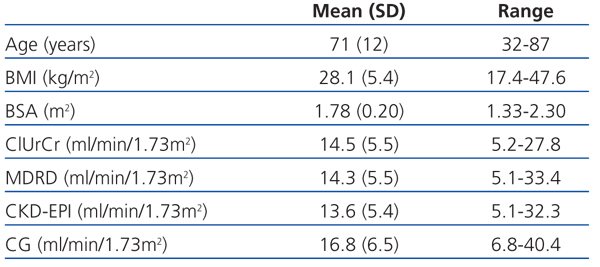
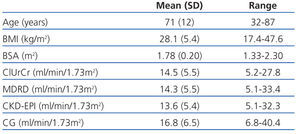
Table 1 summarises the age and anthropometric parameters for our study patients and the glomerular filtration rates obtained using the different methods. We observed no statistically significant difference between the glomerular filtration rate as measured by ClUrCr and the estimate obtained using the MDRD equation (P=.60), but a difference did exist with respect to CKD-EPI (P<.01) and CG (P<.001).
The intraclass correlation coefficient between ClUrCr and the different equations was 0.84 for MDRD, 0.86 for CKD-EPI, and 0.75 for CG. Values above 0.75 indicate an excellent level of concordance.18
We also observed a good correlation between ClUrCr and the different equations used for estimating GFR: r=0.84 for MDRD (P<.001), r=0.86 for CKD-EPI (P<.001), and r=0.82 for CG (P<.001).
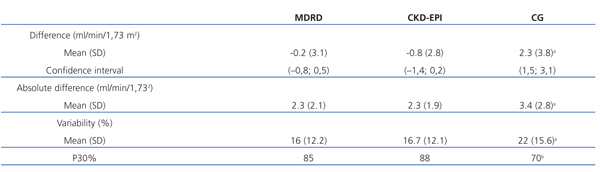
Table 2 shows the values for concordance between glomerular filtration rate as measured using the mean of urine clearance of urea and creatinine and the different estimating equations. MDRD and CKD-EPI had a slight negative bias (mean difference of -0.2ml/min/1.73m2 and -0.8ml/min/1.73m2, respectively). For CG, the bias was positive, with a mean overestimation of glomerular filtration rate of 2.3ml/min/1.73m2. CG was the equation with the greatest level of variability. The value of P30% for CG confirmed that this method had the worse concordance with glomerular filtration rate as measured by ClUrCr. The level of concordance with MDRD and CKD-EPI was similar, and there were no significant differences between these two methods in any of the parameters analysed, except for the difference (P<.01).
The variability in the MDRD and CKD-EPI equations was not influenced by sex, and was not associated with age, body mass index, or glomerular filtration rate as measured by ClUrCr (data not shown). The variability in CG was higher in women (19.3 ± 15.1% in men versus 27.3 ± 15.5% in women; P<.05) and had a negative correlation with age (r=-0.24; P<.05) and glomerular filtration rate as measured by ClUrCr (r=-0.23; P<.05), and a positive correlation with body mass index (r=0.37; P<.001).
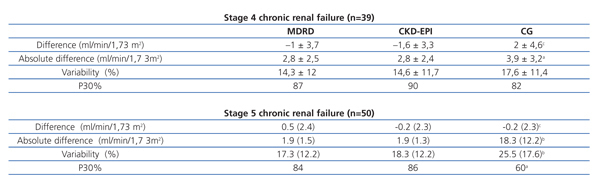
Table 3 shows the results of the concordance analysis based on the stage of chronic renal failure. MRDR and CDK-EPI had a similar level of concordance for both stages analysed. CG had a worse concordance in stage 5 CKD patients.
DISCUSSION
The two main developments in estimating glomerular filtration rates in the past five years have been reduced inter-laboratory variability with standardised creatinine measurements,4 and the appearance of the CKD-EPI equation for reducing the bias inherent in MDRD7 for glomerular filtration rate values greater than 60ml/min/1.73m2. The MDRD equation was re-elaborated in order to adapt it to the new standardised creatinine.5
The aim of our study was to determine whether the CKD-EPI equation was valid in advanced chronic renal failure, specifically in the population treated in our area, with anthropometric characteristics different from those of the North American population, which this formula was designed for.
In 89 patients with stage 4 and 5 chronic renal failure, we have analysed the level of concordance between the MDRD, CKD-EPI, and CG equations with regard to the reference method used for measuring the glomerular filtration rate, which was the arithmetic mean of urine clearance of urea and creatinine.8-11 We only included cases in which, after an interview, we were sure that the urine samples had been taken correctly.
The Pearson’s correlation coefficient, difference, absolute difference, variability, percentage of patients with variability <30%, and the intraclass correlation coefficient all indicate that the CKD-EPI equation has a level of concordance with the reference method similar to MDRD, and superior to the values produced with the classically used CG equation.
These results, produced using standardised creatinine levels, are different from those previously published with MDRD and CG equations in our population with advanced chronic renal disease.3,19 With non-standardised creatinine, the CG equation was more accurate than MDRD for measuring glomerular filtration rate, whether comparing values to the arithmetic mean of and urine urea and creatinine clearance3 or blood clearance of 99mTc-DTPA as reference methods.19 CG was not adapted to standardised creatinine, and lost its capacity for estimating glomerular filtration rates. In our study with advanced chronic renal failure patients, the values obtained using the CG equation with the new creatinine measure tend to overestimate glomerular filtration rate by a mean 2.3ml/min/1.73m2, with a mean variability of 22% (greater than the 16% observed for MDRD and the 16.7% for CKD-EPI), and the percentage of measurements within 30% above or below the value obtained using the reference method was only 70% (this value was 85% for MDRD and 88% for CKD-EPI). Additionally, the variability inherent in the CG equation depends on the sex, age, body mass index (BMI), and glomerular filtration rate of the patient. The accuracy of this value is lower in women, and decreases with lower age and glomerular filtration values, and as BMI increases. On the other hand, the accuracy of the MDRD and CKD-EPI equations is not influenced by these variables. Some authors suggest that the CG equation no longer has clinical relevance, and will not have it until it has been adapted for standardised creatinine and its results have been validated for different populations of patients.20
With the use of a standardised measure of creatinine, MDRD has gained a higher level of concordance with glomerular filtration rate. In a previous study involving non-standardised creatinine in a similar population, the variability for the MDRD equation was 19.3%,3 which has been reduced to 16% in our study using standardised creatinine values. In some studies, a relationship was observed between the bias in MDRD and nutritional state: this equation had a tendency to underestimate glomerular filtration rate in patients with a better nutritional state21 or higher BMI,3 and the accuracy of the equation also depended on the renal failure stage, with greater variability at higher levels of glomerular filtration rate.3 In our study, we did not observe any influence of BMI or stage of renal failure on the parameters for concordance between ClUrCr and the MDRD or CKD-EPI equations.
Levey proposed that MDRD should be replaced by CKD-EPI in all clinical situations,7 which raised a considerable amount of controversy. It is true that the bias, variation, precision, accuracy, and class correlation coefficient for CKD-EPI are very similar to those of MDRD. However, CKD-EPI still does not provide any observable advantage in stage 4 and 5 chronic renal disease patients, and many clinical and epidemiological studies carried out up to the present day have used MDRD.
Keeping in mind the limitations of the sample size, we can conclude that in our population with advanced chronic renal failure, CKD-EPI provides a glomerular filtration rate that is equivalent to that derived from the mean values of urea and creatinine clearance, similar to MDRD. With standardised creatinine, the CG equation has a greater bias and variation and lower precision and accuracy than the other two equations analysed, and its use should therefore be reconsidered.
Acknowledgements
We would like to thank the biostatistics unit for their advice and aid in the statistical analysis of our data.
Table 1. Age and anthropometric variables along with the results from glomerular filtration rates for each method used
Table 2. Concordance study between glomerular filtration rate and the MDRD, CKD-EPI, and CG equations
Table 3. Concordance studies based on the stage of chronic renal failure