INTRODUCCIÓN
La detección precoz de los pacientes con enfermedad renal crónica (ERC) oculta es una de las medidas propuestas por la Sociedad Española de Nefrología (SEN) y otras instituciones en la lucha contra la anunciada epidemia de insuficiencia renal1-3. A los médicos y equipos de atención primaria nos compete una importante responsabilidad en las tareas de identificación precoz de los pacientes con ERC y en la optimización de su tratamiento en fases iniciales, a fin de disminuir el riesgo de progresión de esta enfermedad y su morbilidad cardiovascular asociada. Aunque la determinación de creatinina plasmática sea el método de rutina más universal para valorar la función renal es bien conocido que su relación con el filtrado glomerular (FG) es pobre, precisándose grandes pérdidas de aclaramiento (mayores del 50%) para detectar mínimos incrementos de sus valores plasmáticos4. De hecho, un incremento de la creatinina por encima de los valores considerados normales suele corresponderse con descensos ya importantes del funcionalismo renal, especialmente en mujeres de edad avanzada y en individuos con poca masa muscular5. Esta limitación puede solucionarse con la determinación del aclaramiento de creatinina en orina de 24 horas. Sin embargo este método, además de sobrestimar el FG auténtico, precisa de una correcta recogida de orina, lo que introduce serios inconvenientes para una utilización sistemática en las consultas de asistencia primaria. Por estos motivos las guías de práctica clínica KDOQI (Kidney Disease Outcomes Quality Initiative)6 y la SEN7 recomiendan el uso de ecuaciones predictivas para la estimación del FG. Entre estas ecuaciones destacan las de Cockcroft-Gault8 y las MDRD (derivadas del estudio Modification of Diet in Renal Disease)9. Esta última ecuación tiene la ventaja de no precisar del peso del paciente y es el método de cálculo de FG recomendado por la SEN7, que también preconiza su incorporación rutinaria en los informes de los laboratorios clínicos ante cualquier petición de creatinina plasmática. La mayoría de las comparaciones son favorables a la ecuación MDRD10 pero continúa existiendo controversia y estudios con resultados opuestos12-15.
Con estos antecedentes se diseñó el presente trabajo con dos objetivos. 1) Analizar el grado de concordancia de las ecuaciones de Cockcroft-Gault y MDRD en el diagnóstico de ERC oculta en una cohorte seguida durante 10 años de pacientes de 35 a 74 años, adscritos a un centro de salud urbano, sin antecedentes de enfermedad cardiovascular y cifras normales de creatinina plasmática, y 2) Conocer el perfil de riesgo coronario de los pacientes diagnosticados de ERC oculta en cada una de estas dos ecuaciones de cálculo de FG.
PACIENTES Y MÉTODO
Se realizó un estudio observacional, de seguimiento, en una cohorte retrospectiva de 845 pacientes (4,4% de la población asignada al centro de salud), con edades comprendidas entre 35 y 74 años, sin antecedentes conocidos de cardiopatía isquémica ni de otras enfermedades cardiovasculares, seguidos durante 10 años y con registro todos ellos en su historia clínica, entre el 1-01-1990 y el 31-12-1994, de las variables necesarias para la estimación del FG en la fórmula de Cockcroft-Gault8 y MDRD9 y para el cálculo del riesgo coronario en las ecuaciones de Framingham original16 y REGICOR17. En la ecuación de Cockcroft-Gault se corrigió el FG para una superficie corporal de 1,73 m2, calculada según la ecuación de Dubois y Dubois18. La elección de la función de REGICOR se debió a que esta función, adaptada de la función de Framingham original, ha sido calibrada y recientemente validada en una muestra amplia de población española19. Algunas funciones de cálculo de riesgo de muerte cardiovascular, como la derivada del proyecto INDANA20, incluyen la creatinina sérica entre las once variables utilizadas para el cálculo del riesgo, pero no ha sido validada y se desconoce su aplicabilidad en población española, razón por la que no se incluyó en el presente estudio. Además, las funciones derivadas de Framingham, a pesar de no incluir entres sus factores de riesgo la ERC, parecen discriminar correctamente la probabilidad de eventos coronarios en los pacientes con esta patología21.
Los acontecimientos cardiovasculares investigados en el seguimiento de la cohorte fueron los eventos coronarios (infarto agudo de miocardio y angina objetivada), los accidentes cerebrovasculares y la muerte de causa cardiovascular (coronaria, cerebrovascular o por otras causas cardiovasculares). Para la aceptación de un evento como de origen cardiovascular se exigió la confirmación de su diagnóstico en el ámbito especializado o en el hospital de referencia mediante las pruebas pertinentes (prueba de esfuerzo, talio, coronariografía, etc.). Se consideraron pacientes de riesgo coronario alto aquellos que presentaron un riesgo > 20% en la tabla original de Framingham16 y > 10% en las tablas de Framingham-REGICOR22. Se cumplimentó una hoja de recogida de datos para cada paciente por parte de personal cualificado, una vez definidas y protocolizadas las siguientes variables: cifras de presión arterial sistólica (PAS), presión arterial diastólica (PAD), colesterol total, colesterol unido a lipoproteínas de alta densidad (HDL-colesterol), consumo de tabaco, glucemia, índice de masa corporal (IMC), triglicéridos, colesterol unido a lipoproteínas de baja densidad (LDL-colesterol), consumo de fármacos hipolipemiantes y consumo de fármacos antihipertensivos. La ERC se clasificó en cinco estadios6,23, aplicándose el término ERC oculta cuando el filtrado glomerular estimado fue menor de 60 ml/min (ERC en estadios 3-5)1 con cifras de creatinina plasmática < 1,4 mg/dl en varones y < 1,3 mg/dl en mujeres24. Se excluyeron los pacientes con enfermedad hepática severa, obesidad mórbida (IMC > 40 kg/m2), desnutrición (IMC 18,5 kg/m2) o con amputaciones de miembros7. Finalmente un total de 845 pacientes (8,3% de la población de 35-74 años) reunieron los criterios de inclusión.
Análisis estadístico
El análisis y tratamiento de datos se realizó mediante el paquete estadístico SPSS 12.0 para Windows, el entorno R (versión 2.5.0) y el programa Epi Dat 3.1. Para el análisis descriptivo univariante los parámetros que se utilizaron como representativos de la muestra fueron: media, desviación típica, frecuencias observadas y proporciones en distribuciones normales; y la mediana y los cuartiles 1 y 3 en distribuciones no normales. La normalidad de las variables se comprobó a través del test de Kolmogorov-Smirnov y diagramas de normalidad, estudiándose la homocedasticidad mediante la prueba de Levene. En el análisis bivariante de distribuciones normales se empleó la prueba T para muestras independientes en el caso de variables cuantitativas y la prueba Ji-cuadrado (c2) o el test exacto de Fisher en el caso de variables categóricas. En el estudio bivariante de las variables sin distribución normal se utilizó el test no paramétrico U de Mann-Whitney. El análisis de la concordancia entre las dos ecuaciones de cálculo FG en el diagnóstico de ERC oculta se hizo mediante el índice kappa, considerándose25 que existe un grado de concordancia excelente cuando se obtienen valores entre 0,81 y 1; bueno con valores de 0.61 a 0,80 y moderado con valores de 0,41 a 0,60. Para el análisis de la correlación y concordancia entre las ecuaciones de Cockroft-Gault y MDRD como métodos de medida cuantitativa del FG se utilizó el método de Bland-Altman y el test de Shapiro-Wilk para valorar si la diferencia de medias es significativamente distinta de cero. Finalmente también se obtuvieron gráficos de dispersión, el coeficiente de correlación de Pearson y la recta de regresión.
RESULTADOS
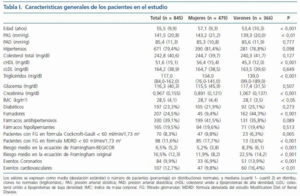
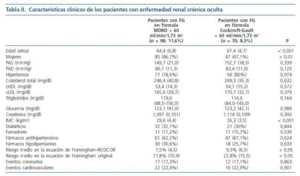
Las características clínicas de los pacientes incluidos en la cohorte se muestran en la tabla I, apreciándose que un 56,7% son mujeres, con un mayor porcentaje de ERC oculta en la fórmula MDRD (17,7% frente a 3,6%, p < 0,001). También las mujeres presentaban mayor edad, cifras de PAS, HDL-colesterol e IMC y un menor riesgo coronario y porcentaje de fumadores que los varones (tabla I). Un 8,3% de la población tendría ERC utilizando la fórmula de Cockcroft-Gault y un 11,6% empleando MDRD. Los pacientes catalogados de ERC oculta en la función de Cockcroft-Gault tienen más edad (67,4 años frente a 64,4, p < 0,001) y un mayor riesgo coronario, tanto en la función de Framingham original como en REGICOR, mientras que los pacientes diagnosticados de ERC por MDRD tienen un IMC más elevado (29,6 frente a 26,3 kg/m2, p < 0,001) y muestran un mayor porcentaje de mujeres (86,7% frente a 67,1%, p < 0,01) (tabla II).
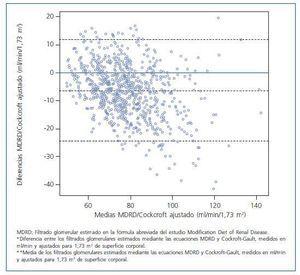
El índice kappa de concordancia entre las dos funciones de estimación del FG en el diagnóstico de ERC oculta fue de 0,55, lo que indica un grado de concordancia moderado. Esta conclusión también se obtiene observando el gráfico de Bland-Altman (fig. 1), apreciándose gran cantidad de mediciones que no se sitúan alrededor de la diferencia igual a cero (p < 0,001). El coeficiente de correlación de Pearson, entre el FG estimado por las ecuaciones de Cockcroft-Gault y MDRD en toda la cohorte, fue de 0,828 (p < 0,001) y de 0,142 (p = 0,327) cuando la relación se limitó a los pacientes con ERC en ambas fórmulas. La recta de regresión entre ambas fórmulas (FG estimado en la ecuación de Cockcroft-Gault = 4,90 + 1,02 MDRD) indica que la estimación del FG mediante Cockcroft-Gault ofrece valores más altos que los estimados con MDRD, en concreto la fórmula de Cockcroft-Gault tiende a dar valores de 4,90 unidades más que MDRD.
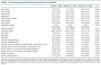
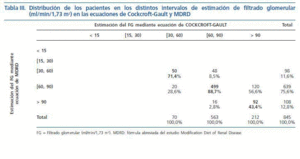
El número y porcentaje de pacientes incluidos en los diferentes intervalos de valores de FG estimados en ambas fórmulas se muestra en la tabla III, observándose como el grado de acuerdo entre las dos fórmulas es mayor en las categorías inferiores de FG. Por ejemplo, un 71,4% de los 70 pacientes con FG < 60 ml/min/1,73 m2 en la ecuación de Cockcroft- Gault son incluidos en el mismo intervalo de FG en MDRD, mientras que solo se incluyeron el 43,4% de los pacientes con FG estimado > 90 ml/min/1,73 m2. También se aprecia como la fórmula de Cockcroft-Gault suele ubicar a un mayor número de pacientes en intervalos de FG más altos respecto a los estimados en MDRD (212 frente a 108 pacientes), mientras que la ecuación MDRD ubicó a un mayor porcentaje de pacientes en categorías de FG inferiores respecto al FG estimado en la fórmula de Cockcroft-Gault (tabla III).
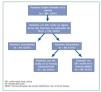
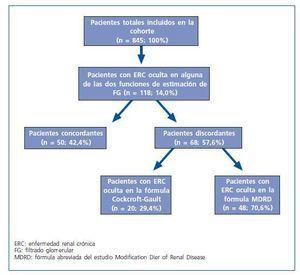
En síntesis, sólo el 42,4% (50 pacientes) de los 118 catalogados de ERC oculta fueron diagnosticados de dicha enfermedad por ambas funciones. De los 68 pacientes diagnosticados de ERC oculta por una sola de las dos funciones, 20 fueron incluidos como portadores de ERC oculta en la ecuación de Cockcroft-Gault y 48 en la MDRD (fig. 2).
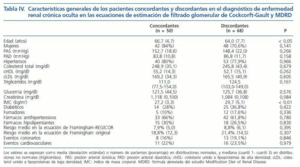
Un 84% de los pacientes concordantes (con ERC oculta en ambas funciones de estimación de FG, tabla IV) son mujeres, con un bajo porcentaje de fumadores (10,0%) y un riesgo coronario moderado en las funciones de Framingham original (18,8%) y REGICOR (7,9%). La comparación entre estos pacientes y los discordantes (catalogados de ERC oculta en una sola de las ecuaciones de estimación del FG) revela una menor edad (64,0 frente a 66,7 años, p < 0,05) y un mayor IMC (29,7 kg/m2 frente a 27,2, p < 0,01) en este último grupo (tabla IV).
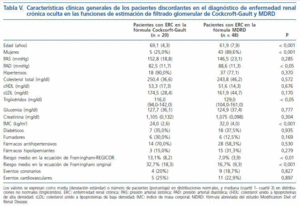
Al comparar los pacientes discordantes entre si, es decir los pacientes que solamente son considerados portadores de ERC oculta en la ecuación de Cockcroft-Gault frente a aquellos que solo son catalogados de ERC en la fórmula MDRD, se aprecia que los pacientes de este segundo grupo son fundamentalmente mujeres (89,6%), con obesidad (IMC 32,0 kg/m2) y con cifras más elevadas de PAD y triglicéridos (tabla V). Por el contrario, los pacientes diagnosticados de ERC oculta exclusivamente con la ecuación de Cockcroft-Gault (tabla V) son fundamentalmente varones (75,0%), con más edad (69,1 frente a 61,9 años, p < 0,001) y un riesgo coronario alto tanto en las funciones de Framingham original (32,7%) como en REGICOR (13,1%).
Durante el seguimiento hubo un mayor porcentaje de eventos en los varones, tanto coronarios (13,9% frente a 6,9%, p < 0,001) como cardiovasculares (16,4% frente a 9,8%, p < 0,01). Sin embargo no hubo diferencias significativas en los porcentajes de episodios coronarios o cardiovasculares entre los pacientes con diagnóstico de ERC oculta en una u otra función de estimación de FG (tablas I y II).
DISCUSIÓN
La ERC constituye uno de los principales problemas de salud pública en la actualidad, tanto por su elevada prevalencia26-28 como por su importante morbilidad cardiovascular y los costes sociales y económicos que conlleva su padecimiento2. La prevalencia de ERC oculta detectada en nuestra población (8,3% con la fórmula de Cockcroft-Gault y 11,6% con la MDRD) está en consonancia con la de otros estudios de nuestro ámbito27,29-31 y de otros países32. También la mayor prevalencia de ERC oculta en las mujeres ha sido confirmada en diferentes estudios29-31. En el estudio EROCAP31, realizado en pacientes atendidos en centros de atención primaria, se encontró una prevalencia de ERC oculta del 7,9%, considerándose normales los valores de creatinina plasmática menores de 1,1 mg/dl en mujeres y 1,2 mg/dl en varones y sin exclusión de los pacientes con IMC extremos. En nuestro estudio, si hubiésemos anulado las restricciones de IMC y aceptado el mismo rango de normalidad de creatinina plasmática, el porcentaje de ERC oculta detectada sería del 5,7% (todos los casos mujeres). Estas pequeñas diferencias pueden justificarse por la diferente edad media y prevalencia de los factores de riesgo cardiovascular en ambas poblaciones, con mayores edades y cifras de diabetes en los pacientes del estudio EROCAP. En cualquier caso, las prevalencias de ERC oculta encontradas en la población atendida en los centros de salud de ambos estudios podrían avalar la necesidad de su detección precoz, para disminuir el riesgo de progresión y la morbilidad cardiovascular que lleva asociada la ERC2. De hecho, la identificación precoz de la ERC en atención primaria permitiría la intervención temprana sobre esta enfermedad y sobre sus factores de riesgo, facilitaría la adopción de tratamientos que limitan la progresión del daño renal y ayudaría a evitar los fármacos que alteran la función renal, reduciendo sus graves consecuencias sociosanitarias1. Pero el alto porcentaje de pacientes hipertensos (66,7%) y diabéticos (28,2%) incluidos en el estudio EROCAP31 y también en el nuestro (79,4% de la población era hipertensa y el 23,2% diabética), así como la edad media en ambos estudios (60,6 y 55,5 años, respectivamente) obligan a cuestionarse si tal vez el cribado de ERC oculta no debería limitarse a pacientes con diabetes, hipertensión arterial o mayores de 55 años, tal como preconizan otros autores hasta la aparición de estudios que demuestren una mejor relación coste-efectividad en población general33.
La determinación aislada de la creatinina plasmática es el método de rutina más universal para valorar la función renal, pero su relación con el FG es pobre, sobre todo en ancianos y especialmente en mujeres26. Estos datos justifican el interés de organismos y sociedades científicas por la introducción sistemática del valor del FG, estimado mediante ecuaciones, en los informes rutinarios de los laboratorios. La fórmula MDRD es la ecuación mejor validada34 y es la ecuación recomendada por la SEN7, aunque otros organismos aceptan como alternativa el uso de la ecuación de Cockcroft-Gault para el cálculo de la función renal35. La falta de estandarización de los métodos de medida de la creatinina y las características de las poblaciones analizadas pueden explicar estas discordancias36.
En nuestro estudio la correlación entre ambas ecuaciones era baja y esto implica un problema importante en el abordaje de la ERC oculta puesto que tiende a seleccionar, al menos según estos resultados, poblaciones diferentes, como también ha sido descrito en otras ocasiones14. Esta dispersión de los valores obtenidos con ambas funciones de estimación del FG no es sorprendente, puesto que ambas fórmulas son aproximaciones diferentes al estudio de la función renal a partir de la medición de la creatinina sérica, estimando la ecuación MDRD el aclaramiento del iothalamato I125 y la de Cockcroft-Gault el aclaramiento de creatinina. Por otra parte, la presencia o ausencia del peso en una y otra fórmula puede condicionar los resultados y explicar en parte las diferencias poblacionales observadas, aunque en nuestro estudio hemos ajustado los valores por superficie corporal18 Sin embargo, aunque la diferencia en las mediciones pudiera ser explicada por el diferente origen de las fórmulas esta explicación no evitaría sus consecuencias, que pueden ser importantes desde el punto de vista práctico cuando el médico tiene que decidir si ha de considerar o no como insuficiente renal a un paciente determinado.
La dispersión de valores observados en el gráfico de Bland-Altman está en consonancia con el discreto índice de concordancia entre ambas ecuaciones en la identificación de pacientes con criterios de ERC oculta (kappa de 0,55). Todos los pacientes con ERC de nuestro estudio tenían valores de FG entre 59 y 30 ml/min/1,73 m2, es decir pertenecían al estadio 3, a la clásicamente denominada insuficiencia renal5,7. Si se acepta que la fórmula MDRD presenta una mayor exactitud diagnóstica7 para valores de FG entre 15 y 60 ml/min/1,73 m2, cabría considerar que los pacientes portadores de ERC oculta en nuestro estudio son fundamentalmente mujeres (86,7%), con edades medias de 64,4 años, con un IMC próximo a la obesidad (29,6 kg/m2) y con un riesgo coronario moderado en las funciones de Framingham original y REGICOR (tabla II). Sin embargo, el análisis de los grupos discordantes, esto es de los pacientes que son catalogados de ERC oculta por una sola de las dos ecuaciones (tabla V) aporta resultados reveladores. Los pacientes que son incluidos como portadores de ERC oculta exclusivamente por la ecuación MDRD continúan correspondiendo fundamentalmente a mujeres (89,6%), obesas (IMC de 32,0 kg/m2) y con un riesgo coronario moderado. Por el contrario, los pacientes con ERC oculta en la ecuación de Cockcroft-Gault (tabla V) son básicamente varones (75,0%), con edades más avanzadas (69,1 años), un alto porcentaje de fumadores (30,0%) y diabetes (35,0%) y con un riesgo coronario alto, tanto en la función original de Framingham (32,7%) como en la calibrada de REGICOR (riesgo coronario del 13,1%). Este grupo de pacientes, constituido mayoritariamente por varones, tiene factores de riesgo cardiovascular suficientes para hacer biológicamente plausible una alta probabilidad de desarrollar ERC. El 20% de ellos sufrió un evento coronario y el 25% algún episodio de tipo cardiovascular durante el seguimiento de 10 años (tabla V), lo que también indirectamente indica que la ERC se comporta como un importante factor de riesgo cardiovascular a nivel individual21. Por lo tanto es muy posible que no se trate de pacientes erróneamente catalogados por la ecuación de Cockcroft-Gault como portadores de ERC oculta. Si se optase por la fórmula MDRD en los informes de los laboratorios se estaría excluyendo a este grupo de pacientes que solo la ecuación de Cockcroft-Gault cataloga como portadores de ERC oculta y con altas probabilidades reales de padecerla, y a quienes se les podría privar de la serie de medidas encaminadas a frenar la progresión de la ERC que la introducción del informe rutinario de la estimación de FG pretende facilitar. Estos datos corroboran, en parte, los hallazgos recientemente publicados respecto a los mejores resultados obtenidos con la ecuación de Cockcroft-Gault en paciente con ERC avanzada (estadios 4 y 5)15. El hecho de que en los grupos discordantes los pacientes catalogados de ERC oculta en la fórmula de Cockcroft-Gault sean fundamentalmente varones (75%) también pudiera estar en relación con el bajo porcentaje de inclusión de mujeres (4%) en el estudio original de estos autores8. Por otra parte, la fórmula MDRD no contiene ningún parámetro antropométrico y por lo tanto no sorprende que su grado de precisión pudiera ser diferente en una población con otras características antropométricas, a pesar del ajuste por superficie corporal, con hasta un 60% de estimaciones discordantes en población anciana37. Nuestros datos animan, tal como recomienda la SEN7 y diversos autores36,38 al desarrollo de nuevas ecuaciones de estimación del FG con mayor exactitud diagnóstica, obtenidas a partir de métodos estandarizados de creatinina y/u otras variables biológicas y a su validación en poblaciones independientes frente a métodos de referencia de medida del FG.
Nuestro estudio tiene limitaciones importantes a considerar. La población incluida no se eligió aleatoriamente, sino en función de que tuviese realizada una historia clínica y registradas las variables necesarias para la estimación del riesgo coronario y del FG en las fórmulas de Cockcroft-Gault y MDRD. En nuestro medio no se disponía de un sistema de historia clínica informatizada. Sin embargo, se hizo una revisión y seguimiento sistemáticos de todas las historias clínicas durante 10 años, con una estrategia de localización y seguimiento que evitase pérdidas de pacientes o de acontecimientos cardiovasculares. Por lo tanto nuestros resultados pertenecen a población atendida e historiada en un centro de salud urbano y pudieran no ser extrapolables a la población general, aunque este aspecto no influya en la comparación entre las dos funciones de estimación del FG analizadas. Tampoco habría de influir en la comparación el hecho de que se trata de un estudio, como el EROCAP31, realizado con un solo corte, de manera que no se diferencian aquellos pacientes que presentaban una alteración transitoria de la función renal de aquellos otros con ERC establecida. Una importante limitación del estudio pudiera estar en una inadecuada identificación y cuantificación de los eventos cardiovasculares acaecidos durante el seguimiento de la cohorte. Sin embargo, la metodología establecida para la búsqueda y para la confirmación de los episodios cardiovasculares, consultando historias clínicas, archivos hospitalarios, el registro civil y contactando con los familiares, fue muy rigurosa, siendo además difícil que acontecimientos de esa naturaleza pasaran desapercibidos a lo largo de un seguimiento de diez años. Finalmente nuestro estudio es observacional y no puede excluirse completamente la existencia de otros factores de confusión no identificados. También, como ocurre en este tipo de estudios, sus resultados solamente pueden ser utilizados para generar nuevas hipótesis.
En resumen, el presente estudio confirma una alta prevalencia de ERC estadio 3 oculta (11,6% con MDRD y 8,3% con la fórmula de Cockcroft-Gault) en pacientes de 35-74 años de edad sin enfermedad cardiovascular. También revela una concordancia moderada entre las fórmulas de Cockcroft-Gault y MDRD, con un diferente perfil de pacientes excluidos según se opte por una u otra fórmula. La elección de la fórmula MDRD dejaría fuera del diagnóstico de ERC a un grupo de población, constituido mayoritariamente por varones (75%), de edades avanzadas (69 años) y un alto riesgo cardiovascular, tanto estimado en las ecuaciones de Framingham original y en REGICOR como confirmado en el seguimiento de diez años.
AGRADECIMIENTOS
Este estudio ha sido financiado por la redIAPP (Innovación e Integración de la Prevención y Promoción de la Salud en atención primaria), red temática de investigación cooperativa G03/170 y con ayuda del Programa de Incentivación de la Investigación en Atención Primaria del Instituto de Salud Carlos III. El segundo y cuarto firmantes del artículo también han recibido una beca predoctoral de la Sociedad Española de Medicina Familiar y Comunitaria.
Tabla 1.
Tabla 2.
Tabla 3.
Tabla 4.
Tabla 5.
Figura 1.
Figura 2.