Las investigaciones clínicas reportadas en la presente revista emplean el marco estándar de las estadísticas frecuentistas basado en las hipótesis de significación (p <0,05). Este método conduce a una dicotomizacion de los resultados como «significativos» o «no significativos» que requieren la evaluación de las hipótesis estadísticas1. Por lo tanto, es importante el uso del enfoque bayesiano, como una forma mejorada de extraer conclusiones estadísticas a partir de datos clínicos dado que facilita la respuesta a la pregunta, ¿cuál es la probabilidad de que el efecto sea concluyente según los datos?, que brinda una mayor validez a las conclusiones significativas. Uno de los métodos más conocidos es el factor Bayes (FB), que estima la probabilidad de una hipótesis en relación con la otra dados los datos (por ejemplo, hipótesis nula vs. hipótesis alterna)1,2, esto permite estimar el peso de la evidencia (10 veces el logaritmo decimal del FB), útil para la toma de decisiones clínicas de hallazgos significativos3,4 (tabla 1).
Valores de la prueba bayesiana A/B
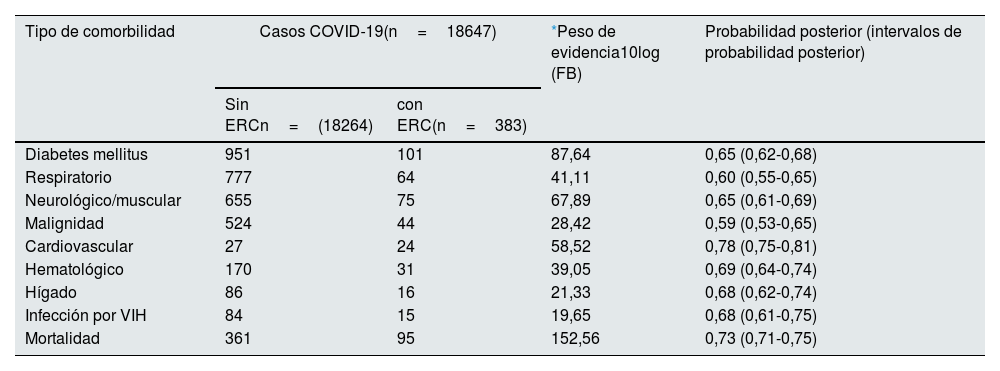
| Tipo de comorbilidad | Casos COVID-19(n=18647) | *Peso de evidencia10log (FB) | Probabilidad posterior (intervalos de probabilidad posterior) | |
|---|---|---|---|---|
| Sin ERCn=(18264) | con ERC(n=383) | |||
| Diabetes mellitus | 951 | 101 | 87,64 | 0,65 (0,62-0,68) |
| Respiratorio | 777 | 64 | 41,11 | 0,60 (0,55-0,65) |
| Neurológico/muscular | 655 | 75 | 67,89 | 0,65 (0,61-0,69) |
| Malignidad | 524 | 44 | 28,42 | 0,59 (0,53-0,65) |
| Cardiovascular | 27 | 24 | 58,52 | 0,78 (0,75-0,81) |
| Hematológico | 170 | 31 | 39,05 | 0,69 (0,64-0,74) |
| Hígado | 86 | 16 | 21,33 | 0,68 (0,62-0,74) |
| Infección por VIH | 84 | 15 | 19,65 | 0,68 (0,61-0,75) |
| Mortalidad | 361 | 95 | 152,56 | 0,73 (0,71-0,75) |
Se recomienda la replicación de los resultados clínicos para validar la credibilidad práctica de tales hallazgos mediante la inferencia bayesiana, útil en diversas pruebas estadísticas (t de Student, odds ratios, regresión lineal o ANOVA)1–3, y en las mediciones diagnósticas como el área bajo la curva ROC (AUCROC) debido a que tales estimaciones son convertibles a un tamaño de efecto, por ejemplo, coeficiente de correlacion (r)5.
Otro modelo bayesiano de interés es la prueba A/B bayesiana para contrastar dos eventos clínicos similares considerando la asignación de distribuciones previas y el control de tales datos muestrales6 según la escala logarítmica de razón de probabilidades (logOR<0, logOR>0), más idónea para la evaluación simultánea con una distribución normal7. El contraste de variación entre ambos grupos proporcionales se representa mediante el FB, esto es útil para diversos estudios que incluyan participantes con y sin el evento clínico de interés, dado que permite evaluar, por ejemplo, las tasas de comorbilidad, ingresos, medicación o mortalidad por COVID-19; cuya aplicación favorece una mayor precisión de las tasas de diferencia en datos a nivel nacional e internacional, donde se reporten probabilidades más realistas mediante la trasformación del tamaño de efecto bayesiano obtenido: OR a probabilidad=OR/(OR+1) y sus respectivos intervalos. Tales estimaciones permiten determinar cuán probable es realmente que los participantes con el desenlace clínico de interés presenten tal ocurrencia. La replicación mediante este método bayesiano es una alternativa para reevaluar hipótesis comparativas de investigaciones con datos binarios o frecuencias que no reporten valores de media ni desviación estándar.
Para la presente carta se consideró los datos reportados de un estudio de la presente revista8, en muestra de pacientes con infección por COVID-19 en diversas comorbilidades, se presentó diferencias significativas entre dos grupos: pacientes con y sin enfermedad crónica renal (ERC). Se tuvo como objetivo determinar la incidencia del desenlace de comorbilidad y el peso de la evidencia (tabla 1).
En la tabla 1 se observa que todos los resultados significativos presentaron estimaciones de evidencia decisiva (>20) a favor de los infectados por COVID-19 con ERC que presentaron condición comórbida de (logOR>0) frente al otro grupo sin esta enfermedad (logOR<0). Los resultados con mayor peso de evidencia fueron los grupos comórbidos de ERC con diabetes mellitus y enfermedad neurológica/muscular, ambos eventos con el 65% de probabilidad de riesgo en contraste a los otros grupos sin ERC. Ser paciente con COVID-19, enfermedad cardiovascular y ERC presentó mayor riesgo de incidencia (78%) frente al otro suceso con un valor de evidencia de 58,52. Otro grupo de riesgo fueron aquellos con COVID-19, enfermedad hematológica y ERC con 69% de ocurrencia y un peso decisivo de 39,05. Adicionalmente se realizó la evaluación de riesgo del evento de mortalidad. La prueba A/B bayesiana reportó un peso de evidencia de 152,56 (decisivo) con una mayor probabilidad de ocurrencia del 73%, cuyos intervalos refieren un mínimo del 71% y un máximo del 75% de riesgo en pacientes COVID-19 con ERC. La replicación estadística mediante la prueba A/B bayesiana ha demostrado su utilidad en otras investigaciones relacionadas con la COVID-199,10, siendo esencial en la elaboración de futuros ensayos biomédicos7,10.